FP: Day 6
Typing
Ken Wakita (https://wakita.github.io/fp2018/)
Oct. 18, 2018
Overview
Compiler Pipeline
Types
MinCaml Types
Figure 2: MinCaml types on page 1, docs/mincaml/overview.pdf

MinCaml Types as 1st-order terms
\[\begin{align} \tau & ::= \\ | & \, \text {bool | int | float} \\ | & \, \mathrm {FunctionalType}(\tau_1, \ldots, \tau_n, \tau) \\ | & \, \mathrm {TupleType}(\tau_1, \ldots, \tau_n) \\ | & \, \mathrm {ArrayType}(\tau) \\ | & \, \alpha \end{align}\]

The MinCaml Typing Rule
Figure 3: MinCaml’s typing rule on page 2, overview.pdf.

The Format of Typing Rules (e.g. let)
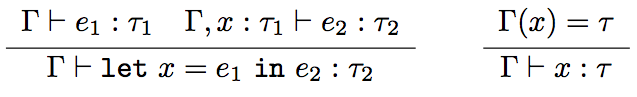
let) and usage- Assumptions
The type of \(e_1\) is \(\tau_1\)
Under a typing environment, where the type of \(x\) is \(\tau_1\), the type of \(e_2\) is \(\tau_2\).
- Conclusion
- The type of \(\texttt {let } x = e_1 \texttt { in } e_2\) is \(\tau_2\).
- Semtanics of
let - The
letform binds a name locally. It introduces a varible \(x\) whose value is the evaluation results of \(e_1\). The scope of \(x\) is \(e_2\) (\(x\) is visible inside \(e_2\)).
Example
Typing let x = 1 in x * 2
\(\Gamma, x:\text {int} \vdash x:\text {int}\) because \(\Gamma, x: \text {int} \vdash \Gamma(x) = \text {int}\).
\(\Gamma, x:\text {int} \vdash 2: \text {int}\) because 2 is an integer constant and the constant rule.
\(\Gamma, x:\text {int} \vdash \texttt {x * 2}: \text {int}\) because of the operator rule for
*, \(\texttt *: \text {int} \times \text {int} \rightarrow \text {int}\).\(\Gamma \vdash 1:\text {int}\) because 1 from the constant rule.
\(\Gamma \vdash \texttt {let x = 1 in x * 2}: \text {int}\), from the last two statements and the typing rule for let.
Typing Rules for let rec
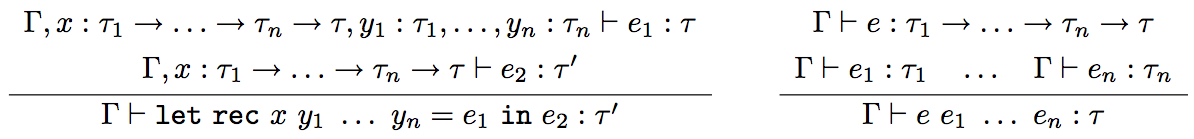
let rec (the LHS)- Assumptions
Under a typing environment where \(x\) is a function whose type is \(\tau_1 \rightarrow \ldots \tau_n \rightarrow \tau\) and the types of \(y_1, \ldots, y_n\) are \(\tau_1, \ldots, \tau_n\), respectively, the type of \(e_1\) is \(\tau\). (When the types of formal and real arguments match, the function’s result type and body’s type should be the same.)
Under a typing environment where \(x\) is a function whose type is \(\tau_1 \rightarrow \ldots \tau_n \rightarrow \tau\), the type of \(e_2\) is \(\tau'\).
- Conclusion
- The type of \(\texttt {let rec } x\ y_1 \ldots y_n = e_1 \texttt { in } e_2\) is \(\tau'\).
Typing Rule for Function Application
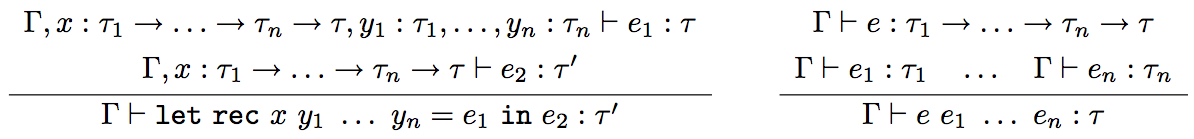
- Assumptions
A function \(e\) takes \(n\) arguments and their types are \(\tau_1, \ldots \tau_n\).
The types of \(e_1, \ldots e_n\) are \(\tau_1, \ldots, \tau_n\), respectively.
These two assumption demand that the types of the formal argument and the actual arguments match.
- Conclusion
- The result type of a function application \(e\ e_1 \ldots e_n\) is \(\tau\).
Implementation of Typing
Typing.deref_...
A series of function that replaces occurrences of type variable by its contents
Typing.deref_typ- Dereferencing of type variables for
Type.t. The essencial code is:
let rec deref_typ = function
...
| Type.Var({ contents = Some(t) } as r) ->
let t' = deref_typ t in
r := Some(t');
t'
...Other code recursively applies deref_* to the subcomponents.
occur r t
Checks if a type varible r occurs in a type expression t.
unify t1 t2
unify t1 t2attempts unification on type variablest1andt2. Instead of computing substitution, type variables are replaced by assignment. This is one rare cases of side effects being used throughout the implementation of the MinCaml compiler.The structure of the
unifyfunction reflects the typing structure, namelyType.t.If it fails to unify
t1andt2, it raises an exception:raise (Unify(t1, t2)).Note: \(x\) and \(f(x)\) are not unifiable.
g env e
g env e examine the structure of e, identifies the typing rule related with that structure, then attempts to unify the assumptions and conclusions of the typing rule with the corresponding structure of e’s type.
The MinCaml Typing Rule
Figure 3: MinCaml’s typing rule on page 2, overview.pdf.
