On treatment of x (1/2)

\[\begin {align} {\cal C}_s&(\text {let rec } x\ y_1 \ldots y_n = e_1 \text { in } e_2 = \\ & {\cal D} \text { += } \mathtt {L}_x(y_1, \ldots, y_n)(z_1, \ldots, z_m) = e_1'; \\ & \begin {cases} \mathit {make\_closure}\ x = (\mathtt {L}_x, ()) \text { in } e_2' \\ \text {where } e_1' = {\cal C}_{s'}(e_1), e_2' = {\cal C}_{s'}(e_2), \\ \text {and } s' = s \cup \{ x \} & \text {when } \mathit {FV}(e_1') \setminus \{y_1, \ldots, y_n\} = \emptyset \\ \\ \mathit {make\_closure}\ x = (\mathtt {L}_x, (z_1, \ldots, z_m)) \text { in } e_2' \\ \text {where } e_1' = {\cal C}(e_1), e_2' = {\cal C}(e_2),\\ \text {and } \{z_1, \ldots, z_m\} = \mathit {FV}(e_1') \setminus \{x, y_1, \ldots, y_n\} & \text {otherwise} \end {cases} \end {align}\]

On treatment of x (2/2)

(* test/cls-bug2.ml *)

let rec f n =
  if n < 0 then () else
  let a = Array.make 1 f in
  a.(0) (n - 1) in
f 9

Application

(* closure.ml *)

let rec g env known = function
  | ...

  | KNormal.App(x, ys) when S.mem x known -> AppDir(Id.L(x), ys)

  | KNormal.App(f, xs) -> AppCls(f, xs)

  | ...

\[\begin {align} {\cal C}_s(x\ y_1\ldots y_n) &= \begin {cases} \mathit {apply\_closure}(x, y_1, \ldots, y_n) & x \not\in s \\ \mathit {apply\_direct}(\mathtt {L}_x, y_1, \ldots, y_n) & x \in s \end {cases} \end {align}\]

The Overview of Closure Conversion

  | KNormal.LetRec({ KNormal.name = (x, t); KNormal.args = yts; KNormal.body = e1 }, e2) ->
    (* Attempt closure conversion, assuming x containing no free variables: Case 1 *)
    if e1' contains free variable (* our assumption is not met *) then
      (* Retry conversion: Case 2 or 3 *)
    (* Generate toplevel function definition *)
    (* Case 1, 3: Create closure *)
    e2'

known and e1' for Case 1, 2

(* Attempt closure conversion, assuming x containing no free variables: Case 1 or 2 *)
let toplevel_backup = !toplevel in
let env' = M.add x t env in
let known' = S.add x known in
let e1' = g (M.add_list yts env') known' e1 in
let zs = S.diff (fv e1') (S.of_list (List.map fst yts)) in
let known', e1' =
  if S.is_empty zs then known', e1' (* confirm that variables are closed in e1' *)
  else Retry conversion because the assertion was not met (* Case 3 *)
    ...
(* Generate toplevel function definition *)
(* Create closure if needed: case 1 or 3 *)
e2'

known and e1' for Case 3

let known', e1' =
  if S.is_empty zs then known', e1' (* confirm that variables are closed in e1' *)
  else (* Retry conversion because the assertion was not met *)
    (toplevel := toplevel_backup; (* reset side effects of conversions for subexpressions *)
     let e1' = g (M.add_list yts env') known e1 in
     known, e1') in

Generation of Toplevel Functions (1/2)

  | KNormal.LetRec({ KNormal.name = (x, t); KNormal.args = yts; KNormal.body = e1 }, e2) ->
    (* Attempt closure conversion, assuming x containing no free variables: Case 1 *)
    if e1' contains free variable (* our assumption is not met *) then
      (* Retry conversion: Case 2 or 3 *)
    (* Generate toplevel function definition *)
    (* Case 1, 3: Create closure *)
    e2'

Generation of Toplevel Functions (2/2)

(* a list of free variables = x, y1, ..., yn *)
let zs = S.elements (S.diff (fv e1') (S.add x (S.of_list (List.map fst yts)))) in
(* free variables with type annotations *)
let zts = List.map (fun z -> (z, M.find z env')) zs in
toplevel := { name = (Id.L(x), t); args = yts; formal_fv = zts; body = e1' } :: !toplevel;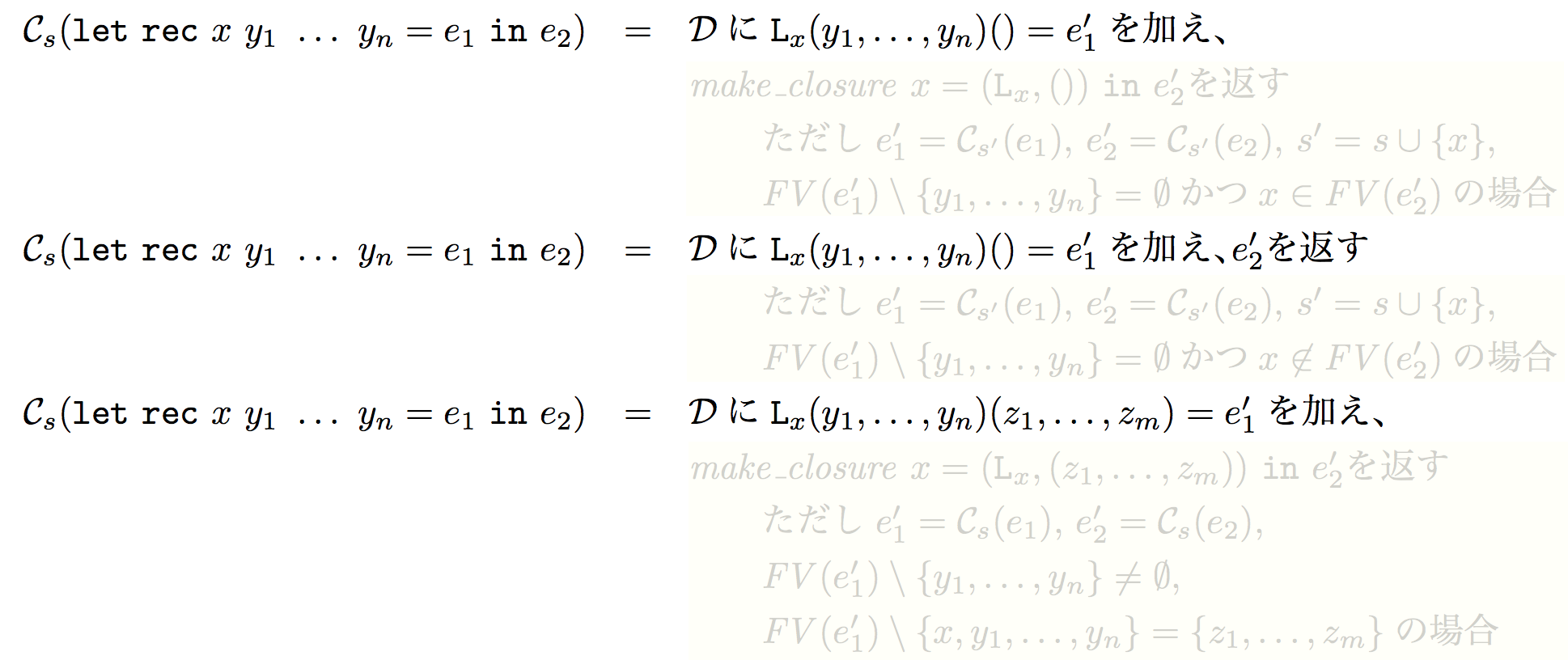

MakeCls and e2' (1/2)

  | KNormal.LetRec({ KNormal.name = (x, t); KNormal.args = yts; KNormal.body = e1 }, e2) ->
    (* Attempt closure conversion, assuming x containing no free variables: Case 1 *)
    if e1' contains free variable (* our assumption is not met *) then
      (* Retry conversion: Case 2 or 3 *)
    (* Generate toplevel function definition *)
    (* Case 1, 3: Create closure *)
    e2'

MakeCls and e2' (2/2)

let e2' = g env' known' e2 in
if S.mem x (fv e2') then (* does x occur in e2' ? *)
  MakeCls((x, t), { entry = Id.L(x); actual_fv = zs }, e2')
else e2'

Issues KW Failed to Answer

1. Aren’t \(\mathit {FV}(e) = \mathit {FV}(e')\) the same?

2. Does S.mem x (fv e2') guarantee \(\mathit {FV}(e_1') \setminus \{y_1, \ldots, y_n\} \not= \emptyset\)?