FP: Day 3
Introduction to OCaml 2
Ken Wakita (https://wakita.github.io/fp2017/)
Oct. 2, 2017
User Defined Types (continued)
Records
A record can be regarded as a tuple whose elements are accessible by names. For example a ratio record as defined below can be regarded as a pair of int’s whose elements are referenced by num and denom.
type ratio = {num: int; denom: int};;A record data constructed by the following syntax:
let r = {num = 12; denom = 15};;And names are used to access its elements:
r.num;;Variant types
Variant types can be used to represent a member of finite flags/sets/states/tags. At first, it may look like enum type in C-like languages. For example, the sign type denotes the domain that is either positive or negative.
type sign = Positive | Negative;;Positive and Negative are called constructors of the sign type.
As we use switch syntax to identify a enum value, we use pattern matching in OCaml:
let sign_int n =
if n >= 0 then Positive
else Negative;;Variant as Tagged Union
Like Java’s Enum type, members of a variant type can have values. In this case, the member’s declaration contains its type: For example, the color type represents colors by several popular colors (black, white, red, …, cyan), and others that are expressed by combinations of red-, green-, blue-intensity.
type color = Black | White | Red | ... | Cyan | RGB of int * int * int;;
let colors = [Black; White; RGB(255, 0, 0); RGB(0, 255, 0); RGB(0, 0, 255)];;We use pattern matching to identify the kind of color type and its value if any.
let color_name c =
match c with
case Black -> "black"
| ...
| RGB(r, g, b) -> Printf.sprintf "RGB(%d,%d,%d)" r g b;;
val color_name : color -> string = <fun>Variants and Recursive Data Types
A recursive data type can be easily defined by referencing the type name being defined in its definition. Let’s look at the definition of the 'a binary_tree type:
type 'a binary_tree =
Empty
| Node of 'a * 'a binary_tree * 'a binary_tree;;
type 'a binary_tree = Empty | Node of 'a * 'a binary_tree * 'a binary_treeIt offers two constructors: Empty represents a leaf of a tree and Node an internal node. The Node constructor contains a triple of a value of type 'a and two subtrees both of type 'a binary_tree.
An Example of a Binary Tree
Node(4, Node(2, Node(1, Empty, Empty), Node(3, Empty, Empty)), Empty)
- : int binary_tree =
Node (4, Node (2, Node (1, Empty, Empty), Node (3, Empty, Empty)), Empty)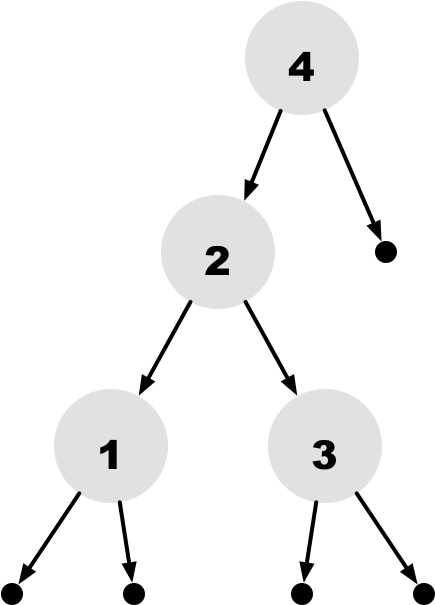
Empty and Node, the label of the circle its value, and arrows references to subtrees.Traversing a Recursive Data
A function that manipulates of trees can simply be defined by use of pattern matching.
let rec member x tree =
match tree with
Empty -> false
| Node(y, left, right) ->
if x = y then true else
if x < y then member x left else member x right;;
val member : 'a -> 'a binary_tree -> bool = <fun>Constructing a Recursive Data
Constructing a recursive data while traversing another. The definition below gives a new binary tree that
let rec insert x tree =
match tree with
Empty -> Node(x, Empty, Empty)
| Node(y, left, right) ->
if x <= y then Node(y, insert x left, right)
else Node(y, left, insert x right);;Exercises
Exercise 1: values
Define a function named values that takes a binary tree and gives a list of values contained in the tree following the order that occur from left to right in the tree.
values Node(4, Node(2, Node(1, Empty, Empty), Node(3, Empty, Empty)), Node(5, Empty, Empty)) should give [1; 2; 3; 4; 5].
An Answer to values
(* This implimentation is not efficient due to its use of the append operator (`@`). The comptational complexity is a square of the size of the tree. Can you guess its worst case scenario? *)
let rec values t =
match t with
| Empty -> []
| Node(x, left, right) -> values left @ [x] @ values right;;A Better Answer to values
(* Efficient solution: linear to the size of the tree *)
let values t =
let rec traverse t values =
match t with
| Empty -> values
| Node(x, left, right) ->
traverse right (x :: traverse left values)
in
List.rev (traverse t []);;Exercise 2: reverse
Define a function named reverse that takes a binary tree and construct a reversed tree which is the mirror image of the given binary tree.
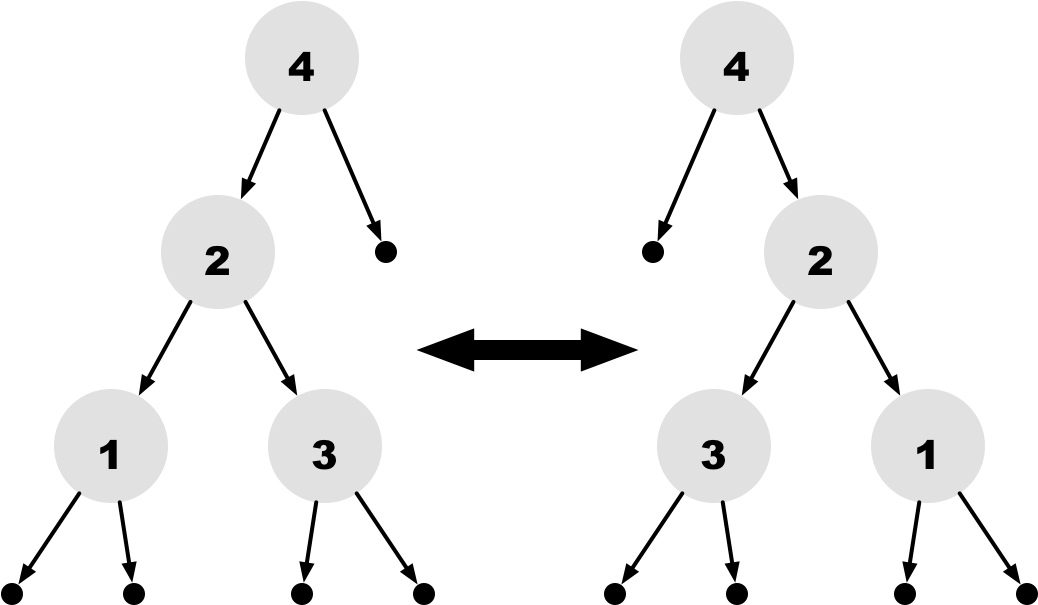
reverse of the treeAn Answer to reverse
let rec reverse t =
match t with
| Empty -> Empty
| Node(x, left, right) -> Node(x, reverse right, reverse left);;Exercise 3: is_binary_search_tree
It is important for the binary search tree that its elements are sorted. If it is not the case the member and insert do not work as we expect: e.g. member 1 (Node(2, Empty, (Node(1, Empty, Empty)))) fails to find 1 contained in the tree.
Define a function name is_binary_search_tree that takes a tree and tells if it is a binary search tree.
An Answer to is_binary_search_tree
let is_binary_search_tree t =
let rec aux test t =
match t with
| Empty -> true
| Node(y, left, right) ->
test y &&
aux (function x -> x < y) left &&
aux (function x -> x > y) right in
aux (function _ -> true) t;;Want more detail?
Complete answers to the exercises:
- Download
03-exercise.ml